Geometría de los Orbitales Atómicos s y p
La conceptualización de los orbitales atómicos representa un cambio paradigmático respecto a los modelos atómicos clásicos. En la mecánica cuántica, la posición de un electrón no puede ser determinada con precisión simultáneamente con su momento (principio de incertidumbre de Heisenberg). En su lugar, describimos la distribución espacial de la probabilidad de encontrar un electrón mediante funciones de onda (Ψ), cuyas soluciones a la ecuación de Schrödinger para un átomo monoelectrónico dan origen a los orbitales atómicos. La densidad de probabilidad electrónica en un punto dado del espacio está dada por el cuadrado del módulo de la función de onda, ∣Ψ∣2.
El Orbital s: Simetría Esférica y Nodos Radiales
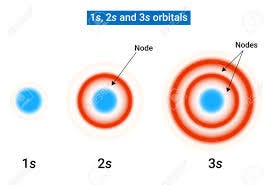
El orbital s (del inglés sharp) es el orbital de menor energía para cada capa principal y se caracteriza por su simetría esférica. Esta isotropía en la distribución de la densidad de probabilidad se debe a que la función de onda para los orbitales s solo depende de la distancia radial (r) al núcleo, y no de los ángulos polares (θ,ϕ).
Nodos Radiales: Los orbitales s con número cuántico principal n≥2 presentan nodos radiales. Un nodo radial es una superficie esférica concéntrica al núcleo donde la probabilidad de encontrar el electrón es cero (Rn,0(r)2=0). El número de nodos radiales para un orbital s es igual a n−1. Por ejemplo, el orbital 1s no tiene nodos radiales, el 2s tiene un nodo radial, y el 3s tiene dos.
La simetría esférica del orbital s lo convierte en un participante clave en la formación de enlaces sigma (σ),
Los Orbitales p: Geometría Direccional y Nodos Angulares
Los orbitales p (del inglés principal) emergen cuando el número cuántico azimutal l=1. Para este valor de l, el número cuántico magnético (ml) puede tomar los valores de -1, 0 y +1, lo que da origen a tres orbitales p degenerados (es decir, con la misma energía) en ausencia de campos externos. Estos tres orbitales se designan comúnmente como px, py y pz, indicando sus orientaciones a lo largo de los ejes cartesianos.
La característica distintiva de los orbitales p es su forma bilobulada, con un nodo planar que pasa a través del núcleo.
Las funciones de onda para los orbitales p exhiben una dependencia angular significativa, representada por los armónicos esféricos Y1,ml(θ,ϕ):
Nodos Angulares: Cada orbital p posee un nodo angular (o planar) que biseca el orbital, pasando por el núcleo. Para el orbital pz, este es el plano xy (donde θ=π/2 y cos(θ)=0). Similarmente, para px es el plano yz y para py es el plano xz. Este nodo angular implica una probabilidad nula de encontrar el electrón en dicho plano.
La presencia de dos lóbulos con signos opuestos en la función de onda (fases de la función de onda) es crucial para la formación de enlaces covalentes, permitiendo interacciones constructivas (enlace) o destructivas (antienlace) con otros orbitales. La direccionalidad de los orbitales p es fundamental para la predicción de la geometría molecular y la formación de enlaces sigma y pi (π).
Implicaciones en la Química Estructural y Reactividad
La comprensión de la forma y la orientación de los orbitales s y p es indispensable para elucidar una multitud de fenómenos químicos:
Hibridación de Orbitales: La hibridación de orbitales atómicos (por ejemplo, sp3, sp2, sp) es un concepto clave en la teoría del enlace de valencia que explica la geometría molecular observada y la valencia de los átomos en las moléculas al generar orbitales híbridos con geometrías y orientaciones específicas que maximizan la superposición orbital.
Formación de Enlaces Sigma (σ) y Pi (π): La superposición frontal y coaxial de orbitales (s-s, s-p, p-p a lo largo del eje internuclear) da origen a enlaces σ, caracterizados por simetría cilíndrica alrededor del eje internuclear. La superposición lateral y paralela de orbitales p (o d) forma enlaces π, que poseen un nodo planar que contiene el eje internuclear. Estas distinciones son críticas para la reactividad y estabilidad de las moléculas.
Teoría del Campo Cristalino y del Campo Ligando: Aunque involucran orbitales d y f, los principios subyacentes a la direccionalidad y la simetría de los orbitales se extienden para explicar el desdoblamiento de los niveles de energía y las propiedades magnéticas y espectroscópicas de los complejos de metales de transición.
La representación de los orbitales atómicos como regiones de probabilidad con geometrías definidas va más allá de una mera abstracción matemática. Provee un marco robusto para comprender la naturaleza de los enlaces químicos, la estereoquímica molecular y, en última instancia, la reactividad de la materia. La capacidad de visualizar y comprender estas distribuciones de probabilidad es una herramienta heurística esencial en la química moderna.